Mathematician and
Software Engineer
About Me
Researcher, Engineer, Tinkerer, Scholar, Philosopher and Hyrox afficionado
- Applied Mathematics
- Scientific Computing
- Data Science
- Software Engineering
- History and Philosophy of Mathematics
- Fitness Sports
(Crossfit, Hyrox, HIIT, Functional)
-
PhD in Applied Mathematics, 2015
Saarland University
-
MSc in Applied Mathematics, 2010
Saarland University
-
BSc in Pure Mathematics, 2008
University of Luxembourg
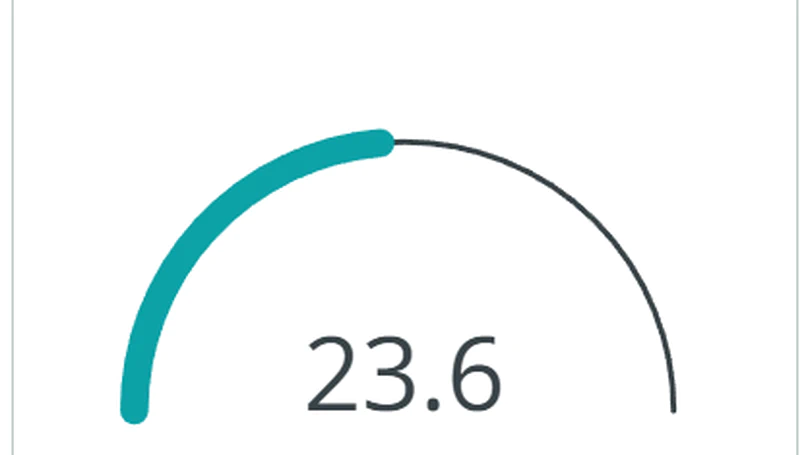
Skills
100%
Computer Vision
95%
Python, Matlab
90%
80%
Data Science
60%
Experience
Accomplishments
Recent Posts
Projects

Recently I acquired a Raspberry Pi 4 and decided to build a tiny computer cluster out of it. The goal is to do play around a bit with parallel computing technology. Some of the things that I will try out are MPI in Fortran Coarray Fortran Parallel computing with julia The Hardware The cluster consists of the following parts (see image above). 1 Raspberry 4 Model B (2GB) equipped with a 16GB MicroSD Card 1 Cluster HAT v2.

Besides my research in computer vision related tasks such as optical flow, photometric stereo, and shape matching and my focus on PDE-based compression, I have also ventured in other image processing tasks. One of these tasks was mathematical morphology. We developed a partial differential equation based leveling model and used a bi-cone shaped colour space to filter our texture in images. In contrast to classical levelling approaches our method also works for well for colour images.

I have used machine learning techniques in various projects. Our most successful applications were in the context of quantizing colour values for optimized inpainting and in accoustic source characterizations. Source Code The source code for clustering methods used for quantizing optimal masks can be found here. The source code for the accoustic source characterization is here.

Let us consider a microphone array comprising $n$ microphones at known locations (see figure above). These microphones register the sound that is emitted by a number of sources with unknown locations. The characterization of these acoustic sources requires the estimation of their location and strength. The propagation of sound from a source position $x$ to a receiver at position $y$ can be modelled by a Green’s function. In the following we assume that the source is always a monopole.

I develop a small toy setup with a pair of Arduinos and some ultrasound sensors to do object localization. The goal is to have at least 4 echo distances in each measurement to assert a unique solution of the localization equations. In addition to the position I also want to compute some validation criteria. The Hardware I’m using two Arduino Unos and 6 HC-SR04 ultrasonic sensors. Each Arduino is in control of 3 sensors and the sensors are placed in two rows of 3 sensors each (see below).

We have investigated high performing optimization algorithms and matrix differential calculus technique in the context of Photometric Stereo and presented the results at the BMVC 2016 Source Code A github repository with the code is maintained by Yvain Quéau. A snapshot (master branch, 2020/12/21) of the repository is available as zip Archive on this website.

I’ve developed optimization algorithms for variational optical flow models based on the split Bregman algorithm in my Master thesis. A follow-up investigation on the necessity of certain intermediate filtering steps was published at the EMMCVPR 2011. I’ve also shown that the optical flow can be used in the context of partial differential equation based image compression. The results were presented in two publications at the SSVM 2019 and in the Journal of Mathematical Imaging and Vision.

The main task in three-dimensional non-rigid shape correspondence is to retrieve similarities between two or more similar three-dimensional objects. We analysed how well partial differential equations may be used to solve this problem. In our approach we used diffusion equations or wave equations that spread over the object surface and used the distribution of the heat/waves as feature descriptors to localize correspondences.

It is possible to compress/inpaint images from very little data. In order to obtain reconstructions that are comparable to the original image it is necessary to optimize the underlying interpolation data. Several such strategies have been discussed in my PhD Thesis. In a series of subsequent publications (here, here and here) we showed the relationship to other partial differential equations and also stated conditions under which the existence of a unique solution can be asserted.
Talks & Posters
Featured Publications

Estimating the shape and appearance of a three dimensional object from flat images is a challenging research topic that is still actively pursued. Among the various techniques available, Photometric Stereo is known to provide very accurate local shape recovery, in terms of surface normals. In this work, we propose to minimise non-convex variational models for Photometric Stereo that recover the depth information directly. We suggest an approach based on a novel optimisation scheme for non-convex cost functions. Experiments show that our strategy achieves more accurate results than competing approaches.

This work analyses several approaches for determining optimal sparse data sets for image reconstructions by means of linear homogeneous diffusion. Two optimisation strategies for finding optimal data locations are presented. The first one impresses through its simplicity and is based on results from spline interpolation theory. However, this approach can only be applied to one dimensional strictly convex and differentiable functions. Due to these restrictions we derive an alternative approach which uses findings from optimal control theory. This new algorithm can be applied on arbitrary signals. Both approaches are analysed for their convergence behaviour. Further, we discuss the problem of selecting good data values for fixed data positions. This problem can be analysed as a least squares problem. An important relationship between the optimal data locations and the data values is derived and we present efficient numerical schemes to obtain these values. Finally, we present a image compression approach based on the findings from this work. Experiments show that is possible to outperform popular compression algorithms.
Recent Publications
Contact
If you want to tell me something, write me an e-mail. My public PGP Key.
Full contact details are also available in the Terms section.